Dynamic Programming

An effective way to solve problems that overlap as well as have optimal substructures is to use Dynamic Programming, which is a technique in computer programming.

This is a method for solving a complex problem by breaking it down into a collection of simpler subproblems, solving each of those subproblems just once, and storing their solutions. The CPU can be made more efficient this way.

These involve repeatedly calculating the value of the same subproblems to find the optimum solution.

Example: Minimum Path Sum

Given a mxn grid filled with non-negative numbers, find a path from the top left to the bottom right, which minimizes the sum of all numbers along its path. You can only move either down or right at any point in time.

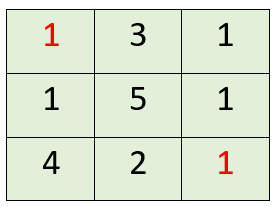
Solution:

Input: grid = [[1,3,1],[1,5,1],[4,2,1]]
Output: 7
Explanation: Because the path 1 → 3 → 1 → 1 → 1 minimizes the sum.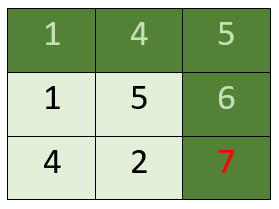

Python Solution

class Solution:
    def minPathSum(self, grid: List[List[int]]) -> int:
        for i in range(len(grid)):
            for j in range(len(grid[0])):
                if i > 0 and j > 0:
                    grid[i][j] = min(grid[i][j] + grid[i-1][j], grid[i][j] + grid[i][j-1])
                elif i > 0:
                    grid[i][j] += grid[i-1][j]
                elif j > 0:
                    grid[i][j] += grid[i][j-1]
        
        return grid[-1][-1]

The intuition behind the approach is that, in order to find the minimum path sum from the top left corner to the bottom right corner of the grid, we can consider the subproblems of finding the minimum path sum to reach each cell of the grid. We can then use the solutions to these subproblems to solve the original problem.

Thus the code implements a dynamic programming approach to find the minimum path sum in a grid.

Different Types of Dynamic Programming Algorithms

1. Longest Common Subsequence

2. Shortest Common Supersequence

3. Longest Increasing Subsequence problem

4. The Levenshtein distance (Edit distance) problem

5. Matrix Chain Multiplication

6. 0–1 Knapsack problem

7. Partition problem

8. Rod Cutting

9. Coin change problem

10. Word Break Problem