Graph-based DSA: Adjacency List

A graph that is represented as an array of linked lists. The index of the array represents a vertex and each element in its linked list represents the other vertices that form an edge with the vertex.

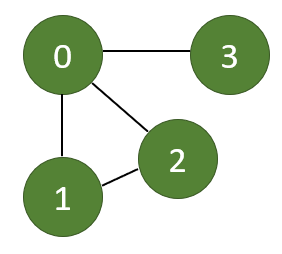
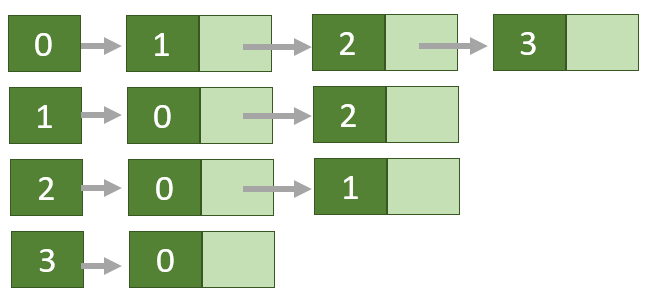
Here, 0, 1, 2, 3 are the vertices and each of them forms a linked list with all of its adjacent vertices. For instance, vertex 2 has two adjacent vertices 0 and 1. Therefore, 2 is linked with 0 and 1 in the figure above.

Nodes = [0, 1, 2, 3]
Adjacency nodes for each node = [[1, 2, 3], [0, 2], [0, 1], [0]]

An adjacency list can be created based on a graph edge list as below.

# Build the adjacency list of the graph
# n = 4
# edges = [[0,1],[0,2],[1,2],[0,3]]

def build_adj_list(self, n: int, edges: List[List[int]])
        adjList = [[] for _ in range(n)]
        for u, v in edges:
            adjList[u].append(v)
            adjList[v].append(u)
            
            print(adjList)    # [[1, 2, 3], [0, 2], [0, 1], [0]]

Adjacency List Code #Python

class AdjNode:
    def __init__(self, value):
        self.vertex = value
        self.next = None


class Graph:
    def __init__(self, num):
        self.V = num
        self.graph = [None] * self.V

    # Add edges
    def add_edge(self, s, d):
        node = AdjNode(d)
        node.next = self.graph[s]
        self.graph[s] = node

        node = AdjNode(s)
        node.next = self.graph[d]
        self.graph[d] = node

    # Print the graph
    def print_agraph(self):
        for i in range(self.V):
            print("Vertex " + str(i) + ":", end="")
            temp = self.graph[i]
            while temp:
                print(" -> {}".format(temp.vertex), end="")
                temp = temp.next
            print(" \n")


if __name__ == "__main__":
    V = 5

    # Create graph and edges
    graph = Graph(V)
    graph.add_edge(0, 1)
    graph.add_edge(0, 2)
    graph.add_edge(0, 3)
    graph.add_edge(1, 2)

    graph.print_agraph()